


 ATAN2_YX_LREAL
ATAN2_YX_LREALDevuelve el ángulo φ de las coordenadas Cartesianas (x,y) con argumentos LREAL
ATAN2_YX_LREAL devuelven el ángulo j de las coordenadas cartesianas (x,y) dentro del rango de -π a +π.

Entrada
Coordenada cartesiana y
Coordenada cartesiana x
Salida
Cada posición P de las coordenadas bidimensionales puede definirse mediante coordenadas cartesianas P(x,y) o mediante coordenadas polares P(r,j) (r = radio, j = ángulo).

Determina ATAN2_YX del siguiente modo:
ATAN2_YX(y,x) |
x |
y |
|---|---|---|
 |
x > 0 |
|
 |
x < 0 |
y ³ 0 |
 |
y < 0 |
|
 |
x = 0 |
y > 0 |
 |
y < 0 |
|
0 |
y = 0 |
Instrucciones F correspondientes: F305_BATAN

Todas las variables de entrada y de salida utilizadas para la programación de esta función han sido declaradas en la Cabecera de la POU. Se utiliza la misma cabecera de la POU para todos los lenguajes de programación.
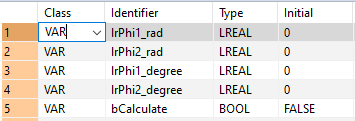
VAR
rPhi1Rad: REAL:=0.0;
rPhi2Rad: REAL:=0.0;
rPhi1Degree: REAL:=0.0;
rPhi2Degree: REAL:=0.0;
END_VAR VAR CONSTANT
DEGR_OF_RAD: REAL:=57.295779513082320876798154814105;
END_VAR
VAR
bCalculatePhi1: BOOL:=FALSE;
END_VAR

BODY
WORKSPACE
NETWORK_LIST_TYPE := NWTYPELD ;
END_WORKSPACE
NET_WORK
NETWORK_TYPE := NWTYPELD ;
NETWORK_LABEL := ;
NETWORK_TITLE := ;
NETWORK_HEIGHT := 3 ;
NETWORK_BODY
B(B_COMMENT,,Calculate the angle values of point in quadrant 2,3,1,32,2,);
L(1,0,1,3);
END_NETWORK_BODY
END_NET_WORK
NET_WORK
NETWORK_TYPE := NWTYPELD ;
NETWORK_LABEL := ;
NETWORK_TITLE := ;
NETWORK_HEIGHT := 5 ;
NETWORK_BODY
B(B_COMMENT,,Result: 2.356194490192345,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,E_ATAN2_YX_LREAL!,,26,0,36,5,,?DEN?Dy?Dx?AENO?C);
B(B_VARIN,,10,24,2,26,4,);
B(B_VAROUT,,lrPhi1_rad,36,2,38,4,);
B(B_VARIN,,-10,24,3,26,5,);
L(1,0,1,5);
L(1,2,9,2);
L(11,2,26,2);
END_NETWORK_BODY
END_NET_WORK
NET_WORK
NETWORK_TYPE := NWTYPELD ;
NETWORK_LABEL := ;
NETWORK_TITLE := ;
NETWORK_HEIGHT := 4 ;
NETWORK_BODY
B(B_COMMENT,,Result: 135.0,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,FP_DEG!,,26,0,32,4,,?DEN?D@'s'?AENO?Cd);
B(B_VARIN,,lrPhi1_rad,24,2,26,4,);
B(B_VAROUT,,lrPhi1_degree,32,2,34,4,);
L(1,0,1,4);
L(1,2,9,2);
L(11,2,26,2);
END_NETWORK_BODY
END_NET_WORK
NET_WORK
NETWORK_TYPE := NWTYPELD ;
NETWORK_LABEL := ;
NETWORK_TITLE := ;
NETWORK_HEIGHT := 3 ;
NETWORK_BODY
B(B_COMMENT,,Calculate the angle values of point in quadrant 4,3,1,32,2,);
L(1,0,1,3);
END_NETWORK_BODY
END_NET_WORK
NET_WORK
NETWORK_TYPE := NWTYPELD ;
NETWORK_LABEL := ;
NETWORK_TITLE := ;
NETWORK_HEIGHT := 5 ;
NETWORK_BODY
B(B_COMMENT,,Result: -0.7853981633974483,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,E_ATAN2_YX_LREAL!,,26,0,36,5,,?DEN?Dy?Dx?AENO?C);
B(B_VARIN,,-5,24,2,26,4,);
B(B_VAROUT,,lrPhi2_rad,36,2,38,4,);
B(B_VARIN,,5,24,3,26,5,);
L(1,0,1,5);
L(1,2,9,2);
L(11,2,26,2);
END_NETWORK_BODY
END_NET_WORK
NET_WORK
NETWORK_TYPE := NWTYPELD ;
NETWORK_LABEL := ;
NETWORK_TITLE := ;
NETWORK_HEIGHT := 4 ;
NETWORK_BODY
B(B_COMMENT,,Result: -45.0,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,FP_DEG!,,26,0,32,4,,?DEN?D@'s'?AENO?Cd);
B(B_VARIN,,lrPhi2_rad,24,2,26,4,);
B(B_VAROUT,,lrPhi2_degree,32,2,34,4,);
L(1,0,1,4);
L(1,2,9,2);
L(11,2,26,2);
END_NETWORK_BODY
END_NET_WORK
END_BODY

//Calculate the angle values of point in quadrant 2
if (bCalculate) then
lrPhi1_rad := ATAN2_YX_LREAL(y := 10.0, x := -10.0); // Result: 2.356194490192345
FP_DEG(s := lrPhi1_rad, d => lrPhi1_degree); // Result: 135.0
end_if;
//Angle value of point in quadrant 4
if (bCalculate) then
lrPhi2_rad := ATAN2_YX_LREAL(y := -5.0, x := 5.0); // Result: -0.7853981633974483
FP_DEG(s := lrPhi2_rad, d => lrPhi2_degree); // Result: -45.0
end_if;