ATAN2_YX_LREAL

Gibt den Winkel φ der kartesischen Koordinaten (x,y) mit LREAL-Argumenten zurück

ATAN2_YX_LREAL gibt den Winkel j der kartesischen Koordinaten (x,y) innerhalb des Bereichs -π bis +π zurück.

Parameter

Eingang

y (LREAL): Kartesische Y-Koordinate
x (LREAL): Kartesische X-Koordinate

Ausgang

VAR_OUT (LREAL): Ergebnis in Radiant

Anmerkungen

Jede zweidimensionale Koordinatenposition P kann über die kartesischen Koordinaten P(x,y) oder die Polarkoordinaten P(r,j) (r = Radius, j = Winkel) festgelegt werden.

Legen Sie ATAN2_YX wie folgt fest:

ATAN2_YX(y,x)	x	y
	x > 0
	x < 0	y ³ 0
	x < 0	y < 0
	x = 0	y > 0
		y < 0
0		y = 0

Verwandte Themen

Verwandte F-Befehle: F305_BATAN

Beispiel

POE-Kopf

Im POE-Kopf werden alle Ein- und Ausgangsvariablen deklariert, die für die Programmierung dieser Funktion verwendet werden. Für alle Programmiersprachen wird der gleiche POE-Kopf verwendet.

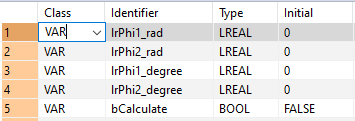
	VAR
		rPhi1Rad: REAL:=0.0;
		rPhi2Rad: REAL:=0.0;
		rPhi1Degree: REAL:=0.0;
		rPhi2Degree: REAL:=0.0;
	END_VAR	VAR CONSTANT 
		DEGR_OF_RAD: REAL:=57.295779513082320876798154814105;
	END_VAR
	VAR 
		bCalculatePhi1: BOOL:=FALSE;
	END_VAR

KOP-Rumpf

BODY
    WORKSPACE
        NETWORK_LIST_TYPE := NWTYPELD ;
    END_WORKSPACE
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 3 ;
        NETWORK_BODY
B(B_COMMENT,,Calculate the angle values of point in quadrant 2,3,1,32,2,);
L(1,0,1,3);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 5 ;
        NETWORK_BODY
B(B_COMMENT,,Result: 2.356194490192345,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,E_ATAN2_YX_LREAL!,,26,0,36,5,,?DEN?Dy?Dx?AENO?C);
B(B_VARIN,,10,24,2,26,4,);
B(B_VAROUT,,lrPhi1_rad,36,2,38,4,);
B(B_VARIN,,-10,24,3,26,5,);
L(1,0,1,5);
L(1,2,9,2);
L(11,2,26,2);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 4 ;
        NETWORK_BODY
B(B_COMMENT,,Result: 135.0,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,FP_DEG!,,26,0,32,4,,?DEN?D@'s'?AENO?Cd);
B(B_VARIN,,lrPhi1_rad,24,2,26,4,);
B(B_VAROUT,,lrPhi1_degree,32,2,34,4,);
L(1,0,1,4);
L(1,2,9,2);
L(11,2,26,2);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 3 ;
        NETWORK_BODY
B(B_COMMENT,,Calculate the angle values of point in quadrant 4,3,1,32,2,);
L(1,0,1,3);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 5 ;
        NETWORK_BODY
B(B_COMMENT,,Result: -0.7853981633974483,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,E_ATAN2_YX_LREAL!,,26,0,36,5,,?DEN?Dy?Dx?AENO?C);
B(B_VARIN,,-5,24,2,26,4,);
B(B_VAROUT,,lrPhi2_rad,36,2,38,4,);
B(B_VARIN,,5,24,3,26,5,);
L(1,0,1,5);
L(1,2,9,2);
L(11,2,26,2);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 4 ;
        NETWORK_BODY
B(B_COMMENT,,Result: -45.0,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,FP_DEG!,,26,0,32,4,,?DEN?D@'s'?AENO?Cd);
B(B_VARIN,,lrPhi2_rad,24,2,26,4,);
B(B_VAROUT,,lrPhi2_degree,32,2,34,4,);
L(1,0,1,4);
L(1,2,9,2);
L(11,2,26,2);
        END_NETWORK_BODY
    END_NET_WORK
END_BODY

ST-Rumpf

//Calculate the angle values of point in quadrant 2
if (bCalculate) then
	lrPhi1_rad := ATAN2_YX_LREAL(y := 10.0, x := -10.0); 	// Result: 2.356194490192345
	FP_DEG(s := lrPhi1_rad, d => lrPhi1_degree);			// Result: 135.0
end_if;

//Angle value of point in quadrant 4
if (bCalculate) then
	lrPhi2_rad := ATAN2_YX_LREAL(y := -5.0, x := 5.0); 	// Result: -0.7853981633974483
	FP_DEG(s := lrPhi2_rad, d => lrPhi2_degree);		// Result: -45.0
end_if;